Finding Node Network Routes: Part One
By Zahur Meerun July 2022. Updated August 2022
Content
Part 1: Laying down the basics
Part 2: Applying our algorithm to a Practical Problem
Part One
Tutorial Objective
This article's objective is to simply explain the algorithm used in finding all possible routes within a network of connected nodes.
There are many articles covering this topic that tend to be more for the more experienced programmer and can be hard to grasp for people who are relatively new to programming.
We will break down the coding process into small parts which can easily be digested so as to understand the core concepts involved. For coding we will use python.
How Can Data be stored?
Data needs to be stored! But how? A tree data structure would be a perfect fit. Just like a tree is made of a root connected to branches and leaves a tree data structure has nodes with key pair values.
Each node represents a location having a unique name (key) and a value. The value can be a list, string, or even a dictionary. Each node can be connected to a node or even a series of nodes with links (edges) just like a tree branch is
connected to leaves.
 The root node is the main node from which all links and nodes will branch out. There are many types of tree data structures, for simplicity
the article will deal with a general tree structure which means a node can be linked to many nodes compared to for example a binary tree where nodes
are limited to two connections.
The root node is the main node from which all links and nodes will branch out. There are many types of tree data structures, for simplicity
the article will deal with a general tree structure which means a node can be linked to many nodes compared to for example a binary tree where nodes
are limited to two connections.


Why Tree's?
Trees are mainly used for searching and sorting as they provide a convenient means to store data hierarchically. In our case, we are more
interested in the searching aspect, more specifically the breadth-first traversal method which we will come to later.
Searching through a tree to find a specific node and its corresponding value in a structured form is of high importance and has several practical uses
in programming from file searching, to finding routes in a road network, and even solving a maze. The algorithm which will be used will focus on finding all routes for a specific node which we
will further refine to obtain the shortest routes between 2 nodes. I guess at this point it isn't that hard to realize one practical use of
such an algorithm! Who wouldn't want to travel from A to B in the shortest time unless it's not the cheapest way! (Which will get to eventually).
Let's Talk Recursion
One important concept while traversing nodes is recursion. Recursion is a programming technique using a function or algorithm that calls itself one or more times until a
specified condition is met. Recursion gives us the ability to search our tree using the same function until all nodes have been explored thus greatly facilitating our task
since we no longer need to write multiple functions to find nodes.
In simple terms, we call our functions again, and again until it's no longer needed. A basic illustration of recursion would be the following code:
The call to our function will continue as long as the stopping condition hasn't been met, in this case, num==0.
def recursive_function(num):
if num == 0: #Stopping condition
return print('The End!')
print(num)
recursive_function(num-1)
recursive_function(5) #Call to our function
Output:
54321"The End!"
Defining our Problem and Solution
First, we start by defining our problem from which a step by step solution can be deduced.
Problem: Obtain all routes for a network of connected nodes.
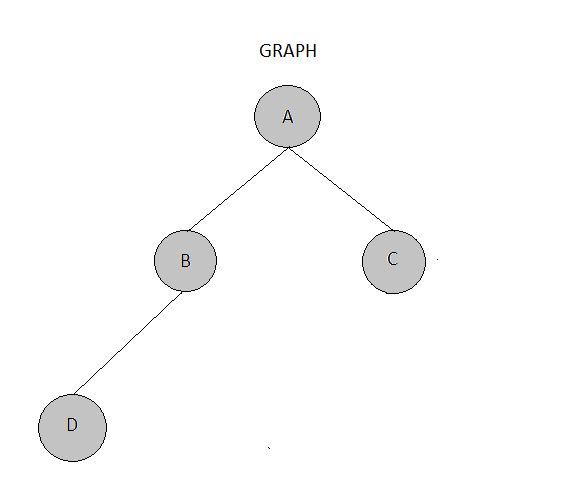
Starting with an initial simple test case ensures that our code works with a minimum of data whilst making debugging more manageable. Hence we will start with the following graph (network) represented by a dictionary:
The following graph can be represented on a diagram as follows:
 Without much effort we can expect the output of the our program to be as detail below, representing all routes starting from node "A":
Our Solution:
Without much effort we can expect the output of the our program to be as detail below, representing all routes starting from node "A":
Our Solution:
Problem: Obtain all routes for a network of connected nodes.
Starting with an initial simple test case ensures that our code works with a minimum of data whilst making debugging more manageable. Hence we will start with the following graph (network) represented by a dictionary:
graph = {"A": ["B", "C"], "B": ["A", "D"], "C": ["A"]}

OUTPUT: [["A", "B", "D"], ["A", "C"]]
1. Starting at the initial node "A" we find all connecting nodes.
 2. Add the accumulated routes from step 1 to a queue, which will consist of the starting node plus the connecting node.
3. The items in the queue our sent back into our functions (recursion!) one by one to check if there are no connecting nodes for the last added node whilst also
checking if the node hasn't been visited before.
2. Add the accumulated routes from step 1 to a queue, which will consist of the starting node plus the connecting node.
3. The items in the queue our sent back into our functions (recursion!) one by one to check if there are no connecting nodes for the last added node whilst also
checking if the node hasn't been visited before.
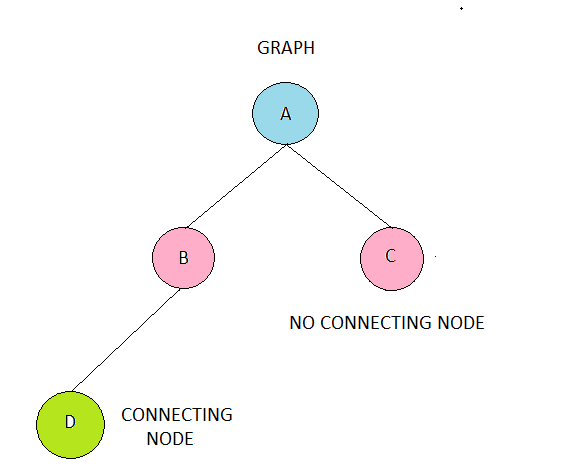 4. If step 3 returns no connecting nodes, therefore implying the queue is empty, we can assume that we have reached the end of our route and we can add that route to a list.
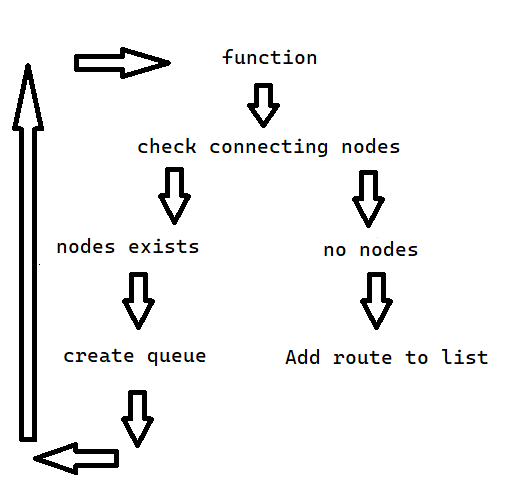
The algorithm used for searching for connecting nodes level by level and is referred to as breadth-first traversal method. The following represents
a flow chart of the algorithm.
4. If step 3 returns no connecting nodes, therefore implying the queue is empty, we can assume that we have reached the end of our route and we can add that route to a list.
The algorithm used for searching for connecting nodes level by level and is referred to as breadth-first traversal method. The following represents
a flow chart of the algorithm.

queue = [["A", "B"], ["A", "C"]]
function(["A", "B"], "B") , function(["A", "C"], "C")

function(["A", "C"], "C") queue empty
We add ["A", "C"] to a list
5. If step 3 yields connecting node/nodes we add the route plus node back to the queue and send it back to our function. This process is continued until no connecting nodes are returned.
queue = [["A", "B" ,"D"]]
function(["A", "B" ,"D"], "D"))
function(["A", "B", "D"], "D") queue empty
queue = []
We add ["A", "B", "D"] to a list
6. Once no connecting nodes are obtained, the queue remains empty signalling the end of the process, we return the list of all routes.
all_routes = [["A", "B", "D"], ["A", "C"]]

Let's Start Coding!
Our code will consist of 2 functions:
1. The Start function will take the initial inputs and send them to our recursive function and will also return our final result. We also require a globally defined variable to store all routes when the queue returns an empty list as described above.
2. The recursive function will be the heart of our algorithm to search through our tree.
Print statements have been included to help us follow our code. Let's run our code using our previously defined graph:
all_routes = []
def find_routes(graph, vertex, visited=[]):
visited.append(vertex)
paths = find_connections(graph, vertex, visited)
return print(f'final result: {paths}')
def find_path(graph, vertex, visited):
queue= []
print(f'Check connections: {visited , vertex}')
for node in graph[vertex]:
if node not in visited:
queue.append(visited + [node])
if queue:
print(f'queue: {queue}')
for route in queue:
find_connections(graph, route[-1], route)
else:
print(f'No Connections!, queue:{queue}'))
print(f'Add to all routes: {visited}')
all_routes.append(visited)
return all_routes
print(f'All Paths: {find_routes(graph, "A")}')
OUTPUT:
Check connections: (['A'], 'A')
queue: [['A', 'B'], ['A', 'C']]
Check connections: (['A', 'B'], 'B')
queue: [['A', 'B', 'D']]
Check connections: (['A', 'B', 'D'], 'D')
No Connections!, queue:[]
Add to all routes: ['A', 'B', 'D']
Check connections: (['A', 'C'], 'C')
No Connections!, queue:[]
Add to all routes: ['A', 'C']
All Paths: [['A', 'B', 'D'], ['A', 'C']]
Output as predicted!
More Test Cases!
Now we know our code is working as expected it's time to increase the pressure and run a slightly more complex test case!
The graph we will use is as follows:
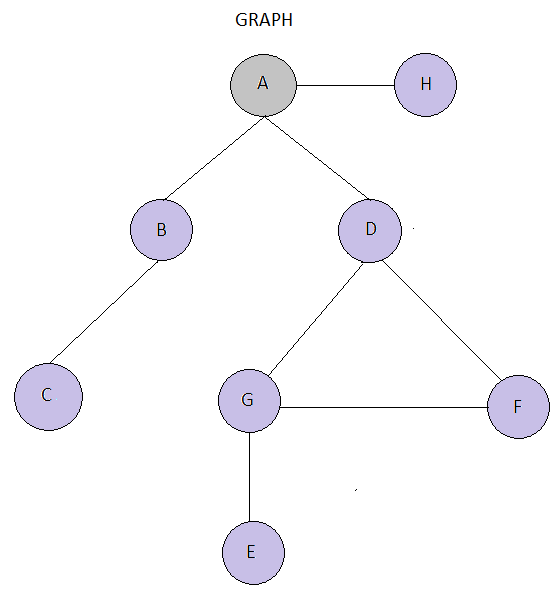 This graph has the added complexity of being cyclic which will further test our code's integrity.
The solution is what we expected, 5 possible routes without revisiting a node.
This graph has the added complexity of being cyclic which will further test our code's integrity.
The solution is what we expected, 5 possible routes without revisiting a node.
graph = { "A": ["B", "D", "H"], "B": ["A", "C"], "C": ["B"], "D": ["A", "G", "F"], "G": ["D", "E", "F"], "E": ["G"], "F": ["D", "G"]}

find_routes(graph, "A")
OUTPUT:
[['A', 'B', 'C'], ['A', 'D', 'F', 'G', 'E'], ['A', 'D', 'G', 'F'],['A', 'D', 'G', 'E'], ['A', 'H']]
Going even further
At this stage, we have returned all possible routes from a node. Although a lot of ground has been covered, our function does not
return something meaningful. Maybe if we could return the shortest distance between two nodes, now that would be helpful. In doing so, the
assumption made is that the shortest distance is always the least amount of nodes we traverse while traveling from start node to end node. This assumption, as we will find
out in part 2 of my tutorial, may not always be true. To extend our functionality I have updated our find_routes function.
def find_routes(graph, vertex, end_node, visited=[]):
visited.append(vertex)
paths = find_connections(graph, vertex, visited)
all_paths = []
for route in all_paths:
if end_node in route:
my_paths.append(route[:route.index(end_node)+1])
path_length = []
for path in my_paths:
path_length.append(len(path))
index_of_minimum = path_length.index(min(path_length))
return my_paths[index_of_minimum]
find_routes(graph, "A", "F")
OUTPUT: ['A', 'D', 'F']
Bonus!
One of the uses of the breadth-first traversal algorithm, as mentioned previously, is solving a maze. Using
the above code I have generated a sandbox where by we can add a start node, end node, and walls and generate
the shortest path from start to finish if a solution exists. The application can be found here.
Conclusion
Great! We started with a network of nodes represented by a graph and returned all 5 possible routes without revisiting a node. From there we further extended our
functionality by returning the minimum path between 2 nodes.
My next tutorial will expand on this topic and apply
what we have learned to a real-life problem, Part 2. This brings us to the end of the tutorial, hope you have enjoyed it. Please send any feedback
by filling out the form below.