Algo

Part 1: Laying down the basics
Part 2: Applying our algorithm to a Practical Problem

In part 1 of this tutorial We started with a network of nodes represented by a graph and returned all 5 possible routes without revisiting a node. We further extended our algorithm by returning the minimum path between 2 nodes. We will now apply what we have learned to a real-life problem

The London Underground would be a perfect example to test our search algorithm by obtaining all paths between 2 points, i.e our departure and destination.

The Tube network is made up of 11 lines, however we will only be interested in 5 lines:

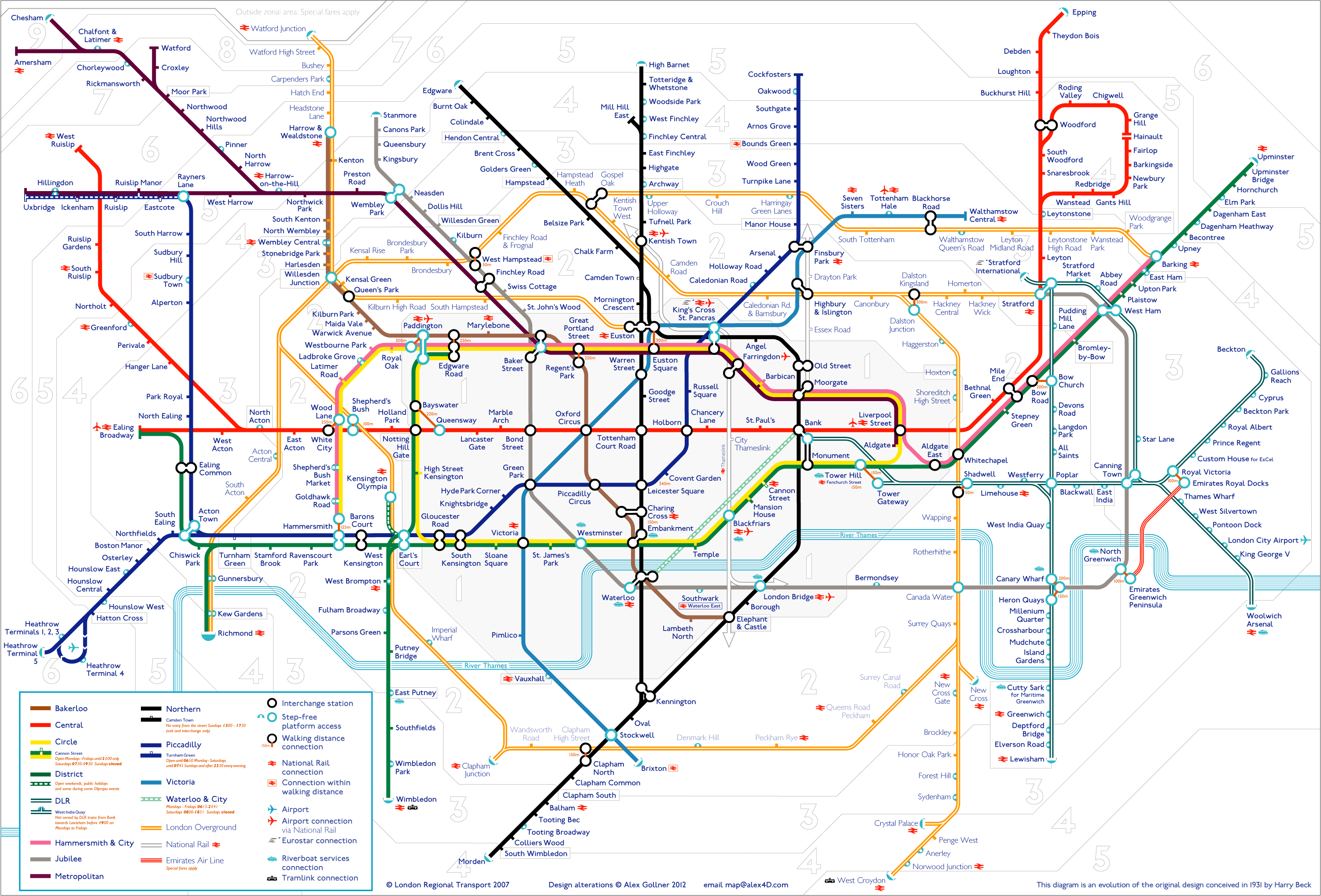
Central Line
Northern Line
Circle Line
Victoria Line
Bakerloo Line

Below is the London Underground Map so you can familiarise yourself with the layout. As you can see, the 5 tube lines cover a vast majority of the network.

Since we can consider each station as a node with edges connecting to other stations, we have a node network similar to what we used in Part 1.

The only difference being that each node (station) is linked to 1 or more Underground lines. To cater for this requirement we can adjust our graph so as each node will contain a key-value pair consisting of a station (key) and another dictionary (value) made up tube line names and connections.

graph = {"Station name": {"Tube name": [list of tubes arriving at this station],
"Connections": [list of all connecting stations]}}

I have assembled the required graph using our 5 chosen lines and linked it here.

We will be using our algorithm derived in part 1 which returned the shortest path available between 2 nodes. We will modify this algorithm to return the 3 shortest paths available.

The steps will be the same as previously described with only a few modifictions to our code. If you wish to have a recap of the code functionality please review Part 1.

Since we have modified our graph to accomodate all tubes lines arriving at our station we will have to update our recursive code to cater for this.

def find_path(graph, vertex, visited):
queue= []

for node in graph[vertex]['Connections']:
if node not in visited:
queue.append(visited + [node])
if queue:

for route in queue:
find_connections(graph, route[-1], route)
else:

all_routes.append(visited)
return all_routes

Secondly we need to modify our initial code to so as to return only the first 3 paths with shortest lengths. We will sort all path retuned from shortest to longest and then add the lines which service these stations, returning only the first 3 paths.

def find_routes(graph, vertex, end_node, visited=[]):
visited.append(vertex)
paths = find_connections(graph, vertex, visited)
all_paths = []
for route in all_paths:
if end_node in route:
my_paths.append(route[:route.index(end_node)+1])
my_paths = sorted(my_paths, key = len)
station_path = []
for path in my_paths:
new_list = [{station: graph[station]["Line"]} for station in path]
station_path.append(new_list)
return station_path[:3]

For our test case we will use departure station as 'Morden' and arrival as 'Stonebridge Park' together with the graph detailed above.

find_routes(graph, 'Morden', 'Stonebridge Park'):
Output:
[[{'Morden': ['Northern Line']}, {'South Wimbledon': ['Northern Line']}, {'Colliers Wood': ['Northern Line']}, {'Tooting Broadway': ['Northern Line']}, {'Tooting Bec': ['Northern Line']}, {'Balham': ['Northern Line']}, {'Clapham South': ['Northern Line']}, {'Clapham Common': ['Northern Line']}, {'Clapham North': ['Northern Line']}, {'Oval': ['Northern Line']}, {'Stockwell': ['Northern Line', 'Victoria Line']}, {'Vauxhall': ['Victoria Line']}, {'Pimlico': ['Victoria Line']}, {'Victoria': ['Victoria Line', 'Circle Line']}, {'Green Park': ['Victoria Line']}, {'Oxford Circus': ['Central Line', 'Victoria Line', 'Bakerloo Line']}, {"Regent's Park": ['Bakerloo Line']}, {'Baker Street': ['Circle Line', 'Bakerloo Line']}, {'Edgware Road': ['Circle Line', 'Bakerloo Line']}, {'Warwick Avenue': ['Bakerloo Line']}, {'Maida Vale': ['Bakerloo Line']}, {'Kilburn Park': ['Bakerloo Line']}, {"Queen's Park": ['Bakerloo Line']}, {'Kensal Green': ['Bakerloo Line']}, {'Willesdon Junction': ['Bakerloo Line']}, {'Harlesdon': ['Bakerloo Line']}, {'Stonebridge Park': ['Bakerloo Line']}], [{'Morden': ['Northern Line']}, {'South Wimbledon': ['Northern Line']}, {'Colliers Wood': ['Northern Line']}, {'Tooting Broadway': ['Northern Line']}, {'Tooting Bec': ['Northern Line']}, {'Balham': ['Northern Line']}, {'Clapham South': ['Northern Line']}, {'Clapham Common': ['Northern Line']}, {'Clapham North': ['Northern Line']}, {'Oval': ['Northern Line']}, {'Kennington': ['Northern Line']}, {'Waterloo': ['Northern Line', 'Bakerloo Line']}, {'Embankment': ['Northern Line', 'Circle Line', 'Bakerloo Line']}, {'Charing Cross': ['Northern Line', 'Bakerloo Line']}, {'Picadilly Circus': ['Bakerloo Line']}, {'Oxford Circus': ['Central Line', 'Victoria Line', 'Bakerloo Line']}, {"Regent's Park": ['Bakerloo Line']}, {'Baker Street': ['Circle Line', 'Bakerloo Line']}, {'Edgware Road': ['Circle Line', 'Bakerloo Line']}, {'Warwick Avenue': ['Bakerloo Line']}, {'Maida Vale': ['Bakerloo Line']}, {'Kilburn Park': ['Bakerloo Line']}, {"Queen's Park": ['Bakerloo Line']}, {'Kensal Green': ['Bakerloo Line']}, {'Willesdon Junction': ['Bakerloo Line']}, {'Harlesdon': ['Bakerloo Line']}, {'Stonebridge Park': ['Bakerloo Line']}], [{'Morden': ['Northern Line']}, {'South Wimbledon': ['Northern Line']}, {'Colliers Wood': ['Northern Line']}, {'Tooting Broadway': ['Northern Line']}, {'Tooting Bec': ['Northern Line']}, {'Balham': ['Northern Line']}, {'Clapham South': ['Northern Line']}, {'Clapham Common': ['Northern Line']}, {'Clapham North': ['Northern Line']}, {'Oval': ['Northern Line']}, {'Stockwell': ['Northern Line', 'Victoria Line']}, {'Vauxhall': ['Victoria Line']}, {'Pimlico': ['Victoria Line']}, {'Victoria': ['Victoria Line', 'Circle Line']}, {'Green Park': ['Victoria Line']}, {'Oxford Circus': ['Central Line', 'Victoria Line', 'Bakerloo Line']}, {"Regent's Park": ['Bakerloo Line']}, {'Baker Street': ['Circle Line', 'Bakerloo Line']}, {'Marylebone': ['Bakerloo Line']}, {'Edgware Road': ['Circle Line', 'Bakerloo Line']}, {'Warwick Avenue': ['Bakerloo Line']}, {'Maida Vale': ['Bakerloo Line']}, {'Kilburn Park': ['Bakerloo Line']}, {"Queen's Park": ['Bakerloo Line']}, {'Kensal Green': ['Bakerloo Line']}, {'Willesdon Junction': ['Bakerloo Line']}, {'Harlesdon': ['Bakerloo Line']}, {'Stonebridge Park': ['Bakerloo Line']}]]

If we were to analyse all the returned paths we can see that the routes returned is as expected. We can even see when a change in tube line occured by following our dictionary! The information returned is useful from a data point of view, however it is not easy to visualize. What if we could transform our algorithm into something more presentable?

Similar to the map sandbox, we will now implement an application allowing us to display our output in a more user-friendly manner. We will make use of forms to input any 2 stations for departure and destination and execute our algorithm in the backend producing a list similar to the output above. We can then iterate and transform our data into a visual representation of our planned route.

Reset Routes

Even though our algorithm returns the path with the least stops, this may not always translate into the minimum time between 2 stations. For example, if we were to use the application with "Morden" as departure and "Tottenham Court Road" as destination, the least path route (path 1) will require us to change trains twice compared to path 2 which requires no change and has 1 more stop. Instinctively, we can deduce that path 2 would most probably be the best option to take in terms of convenience and time. I intend to address this issue in Part 3 of this tutorial where we will introduce time factor into our algorithm.

We have reached the end of this tutorial. I hope you have enjoyed it as much as I have. Please leave any feedback you might have below or request any other tutorials you would like to see.